Exam 1

Wednesday 1/25
7:00-8:30pm

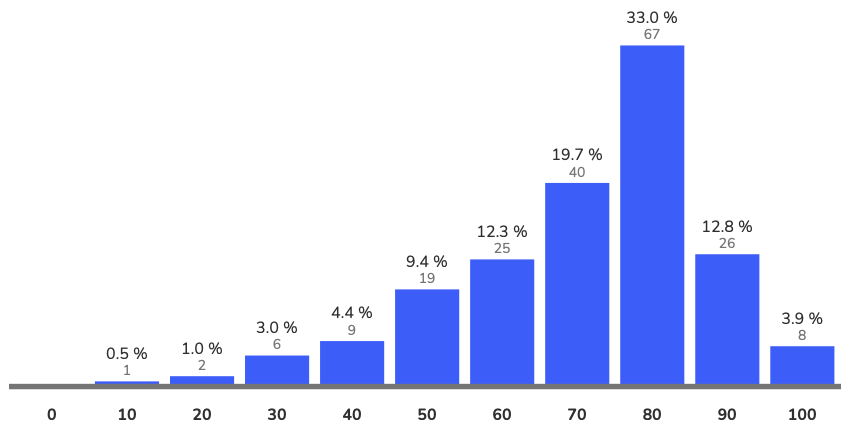
Avg = 75.4


🔑 Here are all the KEYS to Exam 1


Exam protocol All you need to know about HOW to take our online exams.


gchem Chapters:
Chapter 7: Physical Equilibria
Chapter 8: Chemical Equilibria

Learning Outcomes

Chapter 7: Physical Equilibria

Students will be able to...

  1. Demonstrate mastery of and compound and reaction stoichiometry (mole to mole conversion and grams to mole conversions).
  2. Predict the sign of ΔG, ΔH, and/or ΔS for physical change
  3. Understand the concept of spontaneous change and equilibrium in the context of phase changes, including calculating phase transition temperatures from standard thermodynamic data.
  4. Interpret heating curves and calculate heat required for phase transitions and temperature changes.
  5. Describe phase transitions (macroscopically and microscopically).
  6. Understand phase in the context of Boltzmann distribution.
  7. Understand how intermolecular forces, temperature, and solute concentration affect vapor pressure.
  8. Interpret phase diagrams and identify normal boiling and melting point, critical point, and triple point.
  9. Describe the factors that favor the dissolution process in terms of intermolecular forces and thermodynamics (eg.: enthalpies of solution, hydration, lattice energy, entropies of solution, free energy of solution, and temperature).
  10. Describe how T and P (Henry’s Law) each affect solubility.
  11. Define and perform calculations for common concentration units: molarity, molality, and mole fraction.
  12. Perform calculations and understand the concepts of the 4 colligative properties: vapor pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure.
  13. Describe the dissociation of ionic compounds in solution and the effects on colligative properties (van’t Hoff factor, i ).

Chapter 8: Chemical Equilibria

Notice that 8 and 9 are crossed out below. RICE Tables are awesome, but we will push them into the next unit with Acid/Base equilibria.

Students will be able too...

  1. Know the importance of the activity of a species and how it relates to concentration, pressure, and equilibrium.
  2. Write the mass action expression for homogeneous and heterogeneous equilibria.
  3. Determine new values for K when combining multiple reactions.
  4. Know the difference between Kp and Kc and be able to convert between the two.
  5. Describe the relationship between free energy and equilibrium
  6. Convert ΔG to Q, as well as ΔG° to K and vice versa.
  7. Determine if a system is at equilibrium and if not which direction the reaction will shift to achieve equilibrium.
  8. Set up and solve a RICE table for a multitude of various reaction types.
    9.
  9. Calculate the concentration/pressure of all species at equilibrium.
    10.
  10. Given a value of K and all but one equilibrium concentration, determine/calculate the missing concentration.
  11. Show a complete understanding of Le Chatelier's principle.
  12. Predict the response of a reaction to an applied stress (concentration, pressure, volume, temperature) both qualitatively and quantitatively.
  13. Calculate the new value of K when the temperature changes to a new value.

Common Chemistry Knowledge The following are common calculations that you have to know for any chemistry class. I'm a little embarassed including them - but better safe than sorry.

molecular weight = mass of substance
moles of substance

molarity = moles of solute
liters of solution


%conc = mass of solute
mass solution x 100%


molality = moles of solute
kg of solvent


mole fraction of A = moles of A
total moles

Main Equations/Formulas for Exam 1 Note that the student will need to know (memorize) all of the mathematical formulas for the exam. The Periodic Table Handout will only have constants, conversion factors, and data - no formulas.

Chapter 7

\(q = m\cdot C_{\rm s}\cdot \Delta T\)

\(q = m \cdot \Delta H_{\rm transition}\)

\( \ln\left({P_2\over P_1}\right) = {\Delta H_{\rm vap}\over R}\left({1\over T_1}-{1\over T_2}\right) \)

\(\Delta H_{\rm solution} = \Delta H_{\rm lattice} + \Delta H_{\rm hydration}\)

\( C_{\rm gas} = k_{\rm H} \; P_{\rm gas} \)

\(P_{\rm solution} = \chi_{\rm solvent}\cdot P^\circ \)

\(\Delta T_{\rm f} = i\cdot k_{\rm f} \cdot m \)

\(\Delta T_{\rm b} = i\cdot k_{\rm b} \cdot m \)

\(\Pi = i\cdot MRT \)

Help Page on van't Hoff Factor

Chapter 8

aA   +   bB   ⇌   cC   +   dD

mass action =
activity, K aCc aDd
aAa aBb

mass action =
conc, Kc [C]c [D]d
[A]a [B]b

mass action =
press, Kp PCc PDd
PAa PBb

Kp = Kc(RT )Δn

Note: remember to use 0.08206 L atm/mol K
for the value of R in this equation. And that...
Δn = (#mol gas products) – (#mol gas reactants)

\( \ln\left({K_2\over K_1}\right) = {\Delta H_{\rm rxn}\over R}\left({1\over T_1}-{1\over T_2}\right) \)

Heating Curves

heating a substance:     \(q = m\cdot C_{\rm s}\cdot \Delta T\)

Phase changes:     \(q = m \cdot \Delta H_{\rm change}\)

Know how to calculate for various heating scenarios and phase changes. We WILL provide the heat capacities and enthalpies of change that are needed.

Vapor Pressure vs Temperature

Clausius-Clapeyron Equation:    \( \ln\left({P_2\over P_1}\right) = {\Delta H_{\rm vap}\over R}\left({1\over T_1}-{1\over T_2}\right) \)

Your thinking here is that there are 5 variables in this equation. Somehow, we will give you 4 of them and you'll calculate the last one. Also remember... all normal boiling points have vapor pressures equal to 1 atm by definition.

Equilibrium Constant vs Temperature

van't Hoff Equation:    \( \ln\left({K_2\over K_1}\right) = {\Delta H_{\rm rxn}\over R}\left({1\over T_1}-{1\over T_2}\right) \)

Looks almost identical to the CC equation above. However, ΔH in this one can be positive or negative.

Making Solutions (aka: Dissolving stuff)

Rule of Thumb: "Likes Dissolve Likes"

Which means that polar solvents tend to best dissolve polar substances and non-polar solvents tend to dissolve non-polar substances. If you have a mismatch (polar/non-polar), you are most likely going to have INsoluble substances - or put another way: the solubility will be very very low if there is a mismatch in polarities.

Dissolving Solids

When a solid does dissolve, the following must be true:

\(\Delta H_{\rm solution} = \Delta H_{\rm lattice} + \Delta H_{\rm hydration}\)

The lattice energy for a solid, \(\Delta H_{\rm lattice}\), is always +positive the way we use it (expanding the solid into separate molecules or ions). The hydration energy, \(\Delta H_{\rm hydration}\), is always –negative in the way we use it. Most salts when dissolving in water tend to have slightly bigger (magnitude) lattice energies than hydration energies which means that most salts have endothermic heats of solution (\(\Delta H > 0\) or + ).

Dissolving Gases

Because gases have no lattice energy, the heat of solution for all gases is exothermic (\(\Delta H < 0\) or – ). The solubility of a gas in a solvent is directly proportional to the partial pressure of the gas in contact with the solvent. That is Henry's Law. Quantitatively Henry's Law is:

Henry's Law:     \( C_{\rm gas} = k_{\rm H} \; P_{\rm gas} \)

Colligative Properties

Vapor Pressure Lowering

Raoult's Law:     \(P_{\rm A} = \chi_{\rm A}\cdot P_{\rm A}^\circ \) for volatile solvent A and non-volatile solute

Raoult's Law:     \(P_{\rm total} = \chi_{\rm A}\cdot P_{\rm A}^\circ + \chi_{\rm B}\cdot P_{\rm B}^\circ \) for volatile solvent A and volatile solute B

Freezing Point Depression:     \(\Delta T_{\rm f} = i\cdot k_{\rm f} \cdot m \)

Boiling Point Elevation:     \(\Delta T_{\rm b} = i\cdot k_{\rm b} \cdot m \)

Osmotic Pressure:     \(\Pi = i\cdot MRT \)

Remember: All concentration terms will need adjustment with the van't Hoff factor, \(i\), if the solute dissociates into ions (salts).







CH302 · 50520 Principles of Chemistry II


Spring 2023 · © mccord