CH301 S22


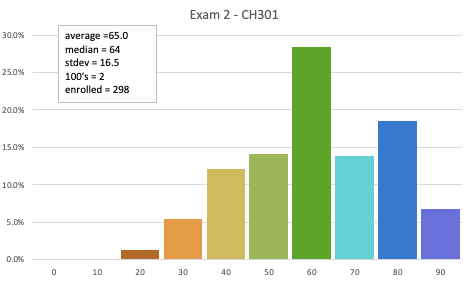
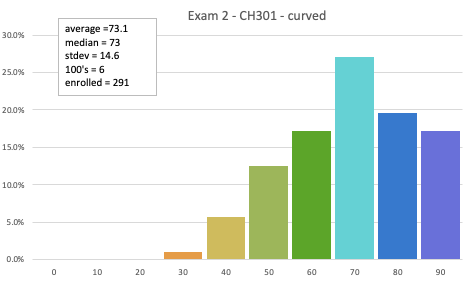
Exam 2

Wednesday 3/9
9:00 - 9:50am




gchem Chapters:
Chapter 1 Section 7: Nomenclature
Chapter 3: Atomic Theory
Chapter 4: Bonding

ChemBook Chapters:
Chapter 1.14 Nomenclature
Chapter 3.8 Nomenclature
Chapter 3: Radiation and Atomic Theory
Chapter 4: Bonding
Chapter 3: Covalent Bonding (Nomenclature)


Learning Outcomes for Atomic Theory (whole chapter - all sections)

Students will be able to...

  1. Perform quantitative calculations based on the relationship between wavelength, energy, and the speed of light.
  2. Identify and rank the different types of radiation which comprise the electromagnetic spectrum.
  3. Explain why classical mechanics doesn't describe electromagnetic radiation.
  4. Describe the photoelectric effect and relate the energy and/or intensity of the photons to the work function and kinetic energy of the ejected electrons.
  5. Explain the origin of atomic and emission spectra and relate these spectra to discrete energy levels.
  6. Apply the Rydberg formula to predict the energy of transitions between fixed energy levels in the hydrogen atom.
  7. Explain that quantum mechanics is a mathematical model, the solutions of which yield wave functions and energies.
  8. List the possible combinations of quantum numbers that are allowed.
  9. State the atomic orbital names based on quantum numbers.
  10. Know the basic shapes of the four types of atomic orbitals (s, p, d, and f).
  11. Know the number of nodal surfaces (planes, cones, and spheres) for the atomic orbitals.
  12. Explain that a wave function can be used to calculate a radial distribution function that describes the probability of an electron as a function of distance away from the nucleus.
  13. Distinguish between one-electron systems and multi-electron systems.
  14. Apply the Aufbau principle to determine the configuration for any atom or ion.
  15. Relate the electronic configuration of an element to its position on the periodic table.
  16. Recognize that there are exceptions to the Aufbau principle and predict where on the periodic table these are likely to occur.
  17. Apply Hund's Rule and the Pauli Exclusion Principle to determine electron configuration using an orbital diagram (electrons in individual orbitals with spins).
  18. Fill an electron atomic orbital diagram and determine whether the element is paramagnetic or diamagnetic.
  19. Apply the shell model of multi-electron atoms to describe the concept of core vs. valence electrons.
  20. Describe the organization of the periodic table and the characteristics of elements in different regions of the table.
  21. Describe the concept of electronic shielding and effective nuclear charge (Zeff) and their relationship to trends in ionization energy, atomic radii, and ionic radii.

NOTE: I've edited this to only show what is possible on Exam 2. .

Learning Outcomes for Bonding (from sections 1-5)
- - specific for Exam 2 - -

Note that NOMENCLATURE is in here as well.

Students will be able to...

  1. Identify metals and non-metals, and predict the types of compounds (ionic/covalent) that will form from different elements.
  2. Distinguish between molecules, ions, and atoms.
  3. Predict the anion or cation that a main-group element is likely to form.
  4. Relate Coulomb’s law to ionic radii, ionic charge, and lattice energy.
  5. Nomenclature IONIC compounds: YES, you will be asked to name an ionic compound and also be given a name and you pick the correct formula. Yes, ALL the polyatomic ions are fair game here.
  6. Describe the distance dependence of the potential energy of a covalent bond.
  7. Predict and explain relative bond strength and lengths in a compound.
  8. Nomenclature COVALENT compounds: Name and write formulas for simple covalent compounds containing 2 different non-metals (like CO is carbon monoxide).
  9. Interpret line drawings of chemical compounds with implicit hydrogens, carbons, and lone pairs.(did this multiple times in class - and the instapoll on Monday 3/7)
  10. Draw the line structure for simple organic compounds with just C, H, O, and N in it. Ok, maybe a halogen or two as well (F, Cl, Br, I).
  11. Rank the polarity of covalent bonds based on relative electronegativity. This is knowing the relative values of ΔEN based on positions in the periodic table.

Formulas YOU should know

electromagnetic radiation: \[c = \lambda \cdot \nu \]

single photon energy: \[E = h \cdot \nu \]

work function: \[E_{\rm k} = {1\over 2} m v^2 = h\nu - \Phi \]

Rydberg formula: \[\Delta E = {\cal R}\left({1\over n_i^2} -{1\over n_f^2}\right) \]

H Energy Levels: \[E_n = -{\cal R}\left({1\over n^2}\right) \]

The Rydberg constant

(\({\cal R}\)) is clearly labeled and given on the Exam Periodic Table Page for Exam 2 which is the front page of your exam copy. Actually, three values are given - use your favorite!

\({\cal R}= 2.18\times 10^{-18} \; \;{\rm J}\)
\({\cal R}= 3.29\times 10^{15} \; \;{\rm s^{-1}}\)
\({\cal R}= 1.097\times 10^{7} \; \;{\rm m^{-1}}\)

EM radiation

light : it's a wave! it's a particle!

Emission vs Absorption

emission: the electron drops down to a lower level and the equivalent amount of energy is released as a photon

absorption: the electron jumps up to higher level and the equivalent amount of energy is absorbed by the electron

Quantum Concepts

total nodes (nodal surfaces actually) in a given orbital    \(= (n-1)\)

angular nodes (cones and planes)    \(= \ell\)

spherical or radial nodes (spheres)    \(= n - \ell - 1\)

Electron Configurations

use the periodic table to follow the Aufbau order

when making cations from transition metals - remove the \(s\) electrons first

Jimmy's Help Videos on Exam 2 topics


Exam protocol All you need to know about HOW to take our in-class exams.