Exam 2 Review Sheet - version 1

Which Chapter/Sections are covered?

The exam covers Chapters 12 and 13. Roughly speaking, the skipped sections in those chapters are 12.6, 12.12, 12.14, 13.3, 13.6, and 13.13. There will also be some general nomenclature stuff (see tables 2.3, 2.4, and 2.5 in your book + LM07 was a review of nomenclature). Oh yeah, due to the very poor performance on the limiting reactant problem on exam 1, we've decided to include another limiting reactant problem on exam 2. So expect a limiting reactant calculation of some sort on this exam. Beside that little addition, you should concentrate on the subject matter that was emphasized in class and on the homeworks and learning modules (H04, H05, H06, LM06, LM07, and LM08). Come in mentally prepared to around 25 to 30 questions. Once again, you need to understand the theory and concepts – getting a homework question right does not necessarily mean you really understand the material. Ask yourself why you chose an answer. Try to explain the question to someone else.

Bring a pencil(s) and non-graphing calculator to the exam. WE will provide you with an exam copy, an answer sheet (bubblesheet), and any scratch paper that you might need.
Know your formulas for calculations. We will provide a list of all constants needed in the formulas. Conversion factors for unit conversions will also be there at the top of the exam. There might even be some extra constants and conversion factors, so just use the ones you need.
Please acquaint yourself with the exam procedures so you'll be ready.
Exam Rooms are the SAME as for Exam 1 and they are given in Quest. Login to Quest and the Announcement will have your exam room listed.

Chapter 2...

Nomenclature

This is clearly stated in section 2.9 of our book. Pay close attention to Tables 2.3, 2.4, and 2.5. My helpsheet on the website duplicates a lot of what you see there although not all of it. There will be a few questions on nomenclature so be prepared. Plus, a question could read... how many available (A) electrons for nitrate? You have to know the correct formula for nitrate to answer this question. The answer is 24 if you must know.

Chapter 12...

Energy traveling at the speed of light

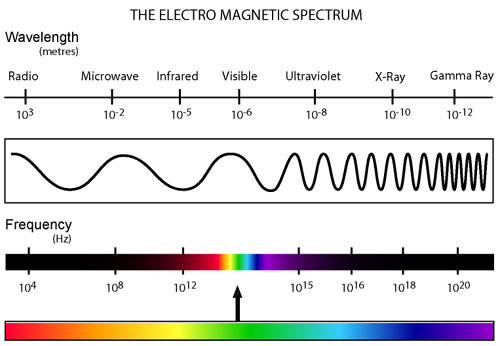
Know what electromagnetic radiation is and how we depict it on the page and conceptually.

Know the basics of the entire electromagnetic spectrum (Figure 12.3 in your book is much like the one shown here which I grabbed off the internet).

Know the approximate wavelengths for each type of radiation given (LOOK at that figure). Know also, that visible light is in the 400-700 nm range (that’s blue end to red end). Other than the two ends, I do not expect you to know the wavelengths of all the colors of the rainbow – however, you SHOULD know the ordering of the colors (think Roy G. Biv).

Use Your Resources - the Internet

Type in “electromagnetic radiation” into a google image search. LOTS of good pictures for learning the relative areas of the scale. Do know what type of excitations go with the various radiation types. For example, visible and UV light yield electronic excitations in atoms and molecules while infra-red (IR) radiation really just causes vibrational excitations. The internet is your friend - use it and you can find countless examples of ALL of this material.

EM Radiation Equations

Know the two views of electromagnetic radiation: as a wave and as a particle (photons). This is best summed up by the two basic equations that we have used to describe electromagnetic radiation:

$$ c = \lambda \; \nu \hskip1in E = h\,\nu $$

Know how to use this equations to calculate various wavelengths, frequencies, and energies of photons. And yes, both c and h values are given on the back of your bubblesheet.

Photoelectric Effect

What is the essence (observations) of the photoelectric effect?

How did Einstein explain this effect?

How does this relate to the work function ($\Phi$) of a metal:

$$ h\nu = \Phi + {\textstyle {1\over2}} mv^2 $$

Be able to calculate any part of this equation ($m, v, \nu, {\rm \;or\;} \Phi$) when given any 3 of the 4 variables in it. Realize that in our textbook (section 12.2), Zumdahl shows the work function term, $\Phi$, as $h\nu_0$. Also be careful here with 'nu' and 'vee'. $\nu$ is frequency, and $v$ is velocity. The symbols look a lot alike but are very different quantities. We will spell out "velocity" or "frequency" on an exam and there will be no ambiguity.

The Emission Spectrum of Hydrogen

KNOW the names of the visible series and the UV series for the hydrogen emission spectrum. Type "hydrogen spectra" into a Google search and LOOK at the image results. Lyman and Balmer are the names - I DID mention them in lecture also.

LOOK at the spectrum and check out those lines. Lines I tell you. Not broad bands of continuous wavelengths but very very narrow precise lines. It’s like hydrogen is speaking to us. What is it saying? It is saying, “I have quantized energy levels!” “When I’m excited, I spit out very specific quanta of energy.” Who listened? Several smart guys but lets chalk one up for Bohr for realizing that the photon that is emitted is due to the energy difference in quantum levels within the atom. As an electron falls from an excited state to a lower energy state, a photon is emitted that corresponds to the energy gap. Balmer looked at the visible spectrum of hydrogen and wrote out an equation to fit the emission lines. Shortly after that, Rydberg came up with a more general equation for the energy levels within the hydrogen atom:

$$E_n = -{{\cal R}\over n^2}$$

Where the Rydberg constant (${\cal R}$) is equal to 2.178 × 10^-18 J (this is what is in your book in section 12.3). You can also divide that by $h$ and have ${\cal R}$ expressed as a frequency ($\nu$) instead of energy, that value is 3.29 × 10¹⁵ s^-1. You can use this equation to calculate all kinds of energies associated with the electronic transitions between the various levels in the hydrogen atom. You just calculate the enery for one level (say $n=x$) and then the energy for another level (say $n=y$), and then take the difference:

$$\nu = {{\cal R}\over n_x^2} - {{\cal R}\over n_y^2} $$

Where x < y. This easily reduces to

$$\nu = {\cal R}\left({1 \over n^2_x} - {1 \over n^2_y}\right)$$

Let’s now count how many different atoms it works for… hmmmm It will work really well as long as you have a nucleus with a charge of +1 and ONE electron somewhere near it. OK, well that’s hydrogen and now your done - answer 1 atom type. OK, so we are somewhat limited here in our equation. The good that comes out of this is that we are now starting to get a more quantitative feel for how energy is in fact quantized within the atom. Note that the '$n$' in that equation is essentially a quantum number. So how do we get a better equation for more electrons? Unfortunately, we will need to increase the complexity of the equation. So yes, the complexity will steeply rise as we proceed through the periodic table and investigate atoms with far more than one electron. The key here is that there WILL be an equation that WILL have quantum numbers associated with it. A better way to go about getting the right equation is to utilize the Schrödinger equation. OK, don’t just utilize it, SOLVE it and find the proper wavefunction ($\psi$) for the electron that you are interested in.

Schrödinger’s Equation

$$ -{\hbar^2\over 2m}{{\rm d}^2\psi \over {\rm d}x^2} + V(x)\psi = E\psi $$

Impressive, isn’t it? And what I show here is for just a one-dimensional problem in dimension "$x$". The Schrödinger Equation is a differential equation. What’s it for? What comes out of it? Can it be solved exactly for all atoms?

The solving of this equation totally depends on setting it up properly. We must mathematically define the boundary conditions for this equation. We’ll use spherical coordinates for this ($r, \theta, \phi$) as described in section 12.7 in your book. Oh my! Check out Table 12.1 for some of the answers ($\psi$’s) that come out of this thing. Scary isn’t it. It's OK, we'll never use those equations. However, we WILL use the three dimensional versions of those equations which are commonly known as the atomic orbitals of the hydrogen atom. Basically, the space around the nucleus is divided up into increasingly complex probability regions known as orbitals. The space is "sliced" and "diced" with planes, cones, and spheres. But ALL of that comes from first solving the Schrödinger equation and identifying the quantum numbers that help define the wavefunctions, $\psi$.

Quantum Numbers

Know the names, symbols, and values (rules) for the four quantum numbers $n$, $\ell$, $m_\ell$, and $m_s$. Also know what each one represents in terms of the electron orbitals of the atom.

principal, $n=1,2,3,\dots$ defines main energy level
angular momentum, $\ell=0,1,2,\dots (n-1)$ defines the shape of the orbital
magnetic, $-\ell \dots -1,0,1,\dots \ell$ defines the spacial orientation of the orbital
spin, $m_s = $ +½ or −½

Out from these quantum numbers and the solution to the Schrödinger equation comes wavefunctions. What does the wavefunction, $\psi$, tell us? Ultimately it allows us to map out in three dimensions the likelihood of finding an electron in a given amount of space. This is what gives us the orbitals of the hydrogen atom that we are (now) all familiar with.

Know your orbitals: name, quantum numbers, shape, numbers, nodal surfaces

Know the basic differences in each orbital type: s, p, d, and f. You should even be able to follow the trend to g, h, i, etc… What do nodes have to do with the shapes of these orbitals? Remember, the total number of nodal surfaces within these orbitals is always equal to $n-1$. What kind of nodes are there in these orbitals? Answer: There are nodal planes and cones (aka: 'angular' nodes), and nodal spheres (aka: radial nodes). How do these influence the shapes of atomic orbitals? How does the most probable distance for the electron vary with different orbitals. You should be able to identify an orbital (1s, 2s, 2p, 3s, etc…) based purely on the number and types of nodal surfaces within it. Check out that Ohio State Chemistry link on our website to get a good idea of how these nodal surfaces give you a 3-dimensional orbital.

How to COUNT nodal surfaces

First, you need to LOOK at the shapes and get them in your head. Each orbital type (s, p, d, and f ) has a specific shape that is governed by the nodals surfaces for that set of quantum numbers.

total nodal surfaces = $n-1$
nodal planes and/or cones = $\ell$
nodal spheres (radial nodes) = $n-\ell-1$

More questions to get straight. What’s the maximum number of electrons that will fit into ANY single orbital? Each orbital type (s, p, d, f . . . ) comes in sets. How many orbitals per set? What is the maximum number of electrons per set? What are the relative energies of the various orbitals for the hydrogen atom? for other atoms? On the exam, READ carefully and know when the question refers to a single orbital or when it refers to an entire set of orbitals.

Electron Configurations

You should be able to write (OK, pick out the answer from a list) out the electron configuration of any element on the periodic table. Yes, you WILL have your own copy of the periodic table to use which will be on the back of the Quest bubblesheet you get. You should also be able to write out electron configurations for various atoms. Remember those spots where there is an exception to the usual filling order (like with Cr and Cu when filling the 3d orbital set.

The Periodic Table

First off, this thing will really help you out with those electron configurations. Make sure you use it when 'memorizing' the Aufbau filling order see Figure 12.31 in your book. Second, you can really learn a lot about elements by studying the trends in the table. Remember that rows are called periods and columns are called families or groups.

Physical Property Trends

Know what the following are (definitions) AND what their trends are on the periodic table: atomic radii, ionization energies, and ~~electron affinities~~. This is section 12.15. A quick reminder here though. For ionization Energy (aka: ionization potential) — you need to also know the difference in first, second, third, etc… what does first, second, and third ionization energies refer to?

Groups and Classifications

Check out Figure 12.39 in section 12.16. Know your group names and what being in a “group” means chemically. We will refer to the representative elements many times when bonding comes along. What are the representative elements? They are the “A” elements on the periodic table (or 1, 2, 13-18). What are the alkali metals and where are they on the periodic table? Where are the alkaline earth metals, the halogens, and the noble gases. Where are the metals, nonmetals, and metalloids? What are the d-transition metals? f-transition metals?

Chapter 13...

Ionic vs Covalent

Know the difference in these two types of bonding and compounds.

Ionic compounds: These are all a continuous lattice of alternating cations and anions. We refer to their identities as formula units and NOT as molecules. They are held together by strong coulombic attractions which leads to nearly all (99.9%) of them being solids at room temperature. Not just solid but brittle solids – they will shatter if you whack them hard enough. If you want to melt them you need to get well above 500˚C and for some, well above 1000˚C. If you do get them melted, the resulting liquid WILL conduct electricity due to all the positive and negative ions flowing around. Let’s not say this: ionic bonds are the transfer of electrons. Yes, we’ve all heard that and it could certainly be the event leading to the formation of ions. However, the fact is simply there are lots and lots of ions (cations and anions) already out there in nature. These ions can and do find one another and they STICK together. THAT my friend is an ionic bond. As far as I’m concerned, the concept of electron transfer is best reserved for oxidation/reduction reactions (redox) and electrochemistry. To say that NaCl is made by taking one electron away from sodium and giving it to chlorine is to speak of an oxidation/reduction reaction – the result of which (in this particular case) is an ionic compound. My point is that you do NOT need to transfer any electrons to get an ionic bond or compound – you need IONS – cations and anions – find them where you may.

Lattice Energies: The lattice energy for a compound is a measure of how much “glue” is holding it together. For ionic compounds (salts), the “glue” is the attractions between cations and anions. Know what this is and what factors increase/decrease the values. Most definitions are for the following type of reaction between gaseous ions to form a solid salt:

$$ {\rm M^+(g) + X^-(g) \longrightarrow MX (s) + energy} $$

The "energy" released in this formula is the lattice energy. So the reaction is shown as an exothermic reaction ($-\Delta H$). Realize that other books show the exact opposite reaction (flip the reactants and product positions) and the reaction is then endothermic ($+\Delta H$). So it is up to you to keep things straight and know that it doesn't matter whether the lattice energy is positive or negative, it is typically thought of in a magnitude sort of way anyway. So we are most concerned with the quantity of energy here.

Lattice energies really follow nicely with Coulomb’s Law which says that the potential energy ($E_P$) between two charges is proportional to the amount of the two charges ($q_1$ and $q_2$) divided by the distance between them ($r_{21}$):

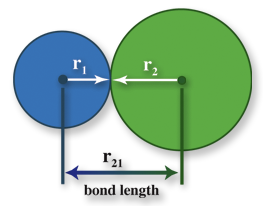
Figure 1

$$ E_P = {q_1 q_2 \over 4\pi \varepsilon_0 r_{21}} $$

That's a pretty involved formula with the pi and the vacuum permittivity constant, $\varepsilon_0$. Let's just simplify things by saying what the proportionalities are:

$$ E_P \propto {q_1 q_2 \over r_{21}} $$

Also, it is important to remember that the bond lengths for all molecules and even ionic compounds are measured nucleus-to-nucleus. This means you add the two radii together to get the bond length. This is shown in Figure 1. For ionic compounds the blue and the green atoms shown would be a cation (+) and an anion (-).

Charge is typically the bigger factor here. Why? Charge can easily double (+2) or even triple (+3). The distance, $r_{21}$, will depend on the size of the ions. The trends you learned in chapter 12 will help you here, but very rarely do you double or triple a ionic radius (although it is possible if you pick the right atoms). Check section 13.4b on ionic radius size... as you go down a group the size goes up by about 25-30% for each jump. Going from left to right is even more subtle: yes, F^- is smaller than O^-2, but only by 4 pm which is very little change.

Covalent compounds: These consist of discrete molecules. These generally are NOT a continuum of covalent bonds (OK, there are network solids which do this – but those are exceptions and are rare in the grand scheme of things). 99.9% of all covalent compounds are molecules – we DO refer to their identities as molecular formulas. They can be solids, liquids, or gases at room temperature. It all depends on their intermolecular forces (we’ll get there soon enough after this exam). Covalent bonds are identified by the sharing of electron pairs by two nuclei.

Lewis Electron Dot Structures

Electron dot structures for ionic compounds show the cation first, then a comma, then the anion. If there is more than one ion in the formula then you put that number in front of the ion. Here is an example of calcium fluoride (CaF2):

Of course MOST of what you’ll be doing is writing out structures for various polyatomic anions and molecules. We’ll ask you questions about the structure – how many lone pairs in all? how many lone pairs on a specific atom? how many bonding pairs? how many total valence electrons in the structure?

S = N - A

I gave you this helpful little formula in class.

S = shared electrons : total number of electrons that will be shared and therefore are the bonding electrons. Divide “S” by 2 and you’ll have the number of bonds (lines) in the structure.

N = needed electrons : needed is based on the octet rule which is 8 electrons for all atoms except hydrogen which is 2. Also, the 8 can (and should) be upped to 10, or 12 for those elements with expanded octets. We'll stick with the true octet rule on this exam. Expanding the octet will come later on exam 3.

A = available electrons : actual number of valence electrons that each atom brings to the structure. Remember to adjust your total up or down here if you have an anion (up) or a cation (down).

What does the formula “S = N – A” do for you? Does it work on ALL structures? It will work on this exam really well... later you will find that you have to sometimes expand the octet rule to 10, 12 or 14. But for exam 2, well keep it simple - The OCTET RULE RULES.

One way to get the right structure:

Get your skeletal structure drawn – remember that symmetry is good.
“Glue” the atoms together with single bonds.
Now use your remaining electrons to fill out the octets on all the atoms.
If you come up short (ran out of electrons before you reached all the octets), you MUST start introducing multiple bonds into the structure – do this until you get the octets you need for all the atoms.
If you actually get the octets taken care of (all atoms are satisfied with complete octets) AND you have some left over electrons put them on the central atom as lone pairs.
Be sure and check formal charge (see discussion later on this review sheet) as your final check on your structure – the more atoms at zero (or close to it) the better. Remember that “sub-octet” atoms like B have only three valence electrons and generally make only three bonds. “expanded-octet” atoms like S may make six bonds. If you minimize the formal charges you will always find the “best” structure even for these octet rule “exceptions”. Oh, but remember, exam 2 will stick with the octet rule in its purest form - 8 electrons.

Bond Order: You can quickly look at a structure and know the bond orders of each bond. Single bonds have bond orders of 1.0, double bonds have bond orders of 2.0, and so on. Can you get fractional bond orders? Yes, but in order to show a fractional bond order we must develop a way to show these things. Lewis dot structures (solo ones) by themselves do not allow for cutting up bonds like 1.5 or 1.25 bonds. That’s one of the reasons why we have resonance structures. Also, looking even further into the chapter 14, bond order is very simple to “calculate” when using MO Theory. It is simply the number of bonding electrons minus the number of antibonding electrons quantity divided by two (section 14.2a).

Radicals: The book DOES talk about ODD electron species (like NO for example). You cannot obey the octet rule with an odd number of electrons. This also means there will be at least one unpaired electron in the structure, which is what a free radical is. ALL odd numbered electron species are radicals. Not having a true octet is the opposite of stabilizing - so radicals are very unstable species. They often reactant quickly with things around them to find a more stable state - like one with an octet of electrons. Most even numbered electron species are not radicals and have all their electrons paired in the structure.

Resonance

Know what resonance is. What are resonance structures and how do we depict them on the page? See section 13.11 in our book. Please realize that in every single case of resonance, all the structures have the EXACT same skeletal structure (where the atoms are). What is different is WHERE the multiple bonds go (and potentially lone pairs). The double bond could go here, or here, or here, etc… The equivalent choices for the double (or triple) bonds effectively show that those electrons are in fact delocalized about the molecule. Resonance structures also allow us to show bond orders other than perfect integers. Consider nitrate ion, NO₃^-. The double bond is delocalized over 3 different oxygens. The bonds to all the oxygens are actually all identical and have bond orders of 1.33 each. That is essentially an average of the three structures shown. Delocalized bonding is handled best by MO Theory in that there are actual molecular orbitals that cover the entire delocalized region (see figure 14.51 in our book for the π-bonding system in nitrate).

Formal Charge

Know how to “calculate” formal charge. WE WILL ask at least one question on formal charge, maybe more.

First, know the “kernel charge” which is the same as the regular number of valence electrons. It’s the number of the group on the American periodic table. The kernel charge is positive due to the nucleus being positive.

Next, you assign electrons to each atom in the formula:

Lone pair electrons belong completely to the atom that they are on.
Bonding electrons are perfectly split between the two atoms that make the bond.

formal charge = kernel charge - assigned electrons

The SUM of all the formal charges in a species must equal the overall charge of the species. For example, all the formal charges in acetic acid (CH₃COOH) must total to zero because it is a neutral molecule. The sum of the formal charges in sulfate (SO₄^2-) must equal -2.

In general, we’d like to see as many formal charges of zero as possible in a formula. A formal charge of zero is giving you the “best” covalent structure possible with electron sharing at its optimum setting so to speak. You can’t always have all zeroes though. Sometimes we HAVE to go to positive or negative formal charges. Values of +1 and -1 are OK when necessary – like for charged species and when you just can’t get all zeros to work out. +2, -2, and beyond are less acceptable though – try to avoid them in your formulas if you truly want a covalent compound. For p-block elements (atoms) beyond phosphorus, there is the possibility of having an expanded octet (10 or 12 usually – could go higher even). The formal charge “rule” will often force you to expand your octet on the central atom to 10 or 12 electrons. Remember, if asked to pick the most likely structure or the best structure - pick the one with the least amount of formal charges. Break any "ties" in importance by picking the structure that puts the more negative formal charge on the more electronegative species. Also remember that although you might have found the MOST important structure, it might not be the ONLY structure necessary to illustrate the proper representation of the molecule. There could possibly be other resonance structures. The structure with the lowest formal charge per atom is the one that contributes the most to the structure, however, the other structures (with more charges) will simply contribute less to the overall structure.

Bond Lengths and Strengths

Know the trends in bond strengths. How does a single bond relate in strength to a double bond? Triple bond? Bond lengths? Take a peak at Table 13.7 in your book. Strengths are often shown in a table of average bond energies (Table 13.6 in your book). Don't try to memorize the table, but DO memorize the approximate range of numbers (energies in kJ/mol) of all the bond types there. It is a good thing to have a good idea about what size a bond energy is.

Class Matters

Attending class does matter. Anything I told you in class is fair game on an exam. Turns out that about 97% of what I tell you is in the book - so if you know the book and what it preaches, then you’ll do fine. If I ever tell you in class about a good exam question, you should wake up and take note. I generally don’t kid about this stuff. Those who are alert and pay attention can reap the rewards.

Standard Disclaimer

Any mistakes on this review sheet are NOT intentional. You should crosscheck all stated information. You should double check your book too.