Review Sheet - Exam 4 - McCord CH301
Which Chapter/Sections are covered?
Chapter 9 sections 1-6 and Chapter 10 sections 1-9, 12-13. Plus Bond Energies (Chapter 13, Tables 13.6 and 13.7 - don’t memorize them but DO know how to use them to calculate \(\Delta H\) of a reaction).
Disclaimer: Although I do my best to avoid mistakes, there could be some on this review. It is YOUR responsibility to cross check all the equations and facts here. If you find and error, correct it and let me know and I'll correct it. No exam question will be thrown out because of anything on or off this review sheet. - Dr. McCord
Equations: NO equations will be given on the exam,
you must know all the equations. I will provide any data and constants needed.
- Dr. McCord

Hydrocarbons and their Combustion Reactions
Make sure you know how to completely write out the chemical equation (balanced) for a combustion reaction. Remember that all hydrocarbons (alkanes) react with oxygen gas to give carbon dioxide and water. When done at 25°C, the water will be liquid, at or above 100°C the water will be gas phase. All the C's become CO2's and all the H's become H2O's. Any oxygen in the formulas just become one of the many oxygens in the CO2 and H2O.
Also know the "heat of combustion" is the amount of heat released from a combustion reaction. Heats of combustion are always positive because we define them as the "amount of heat" released. The actual \(\Delta H\) for a combustion reaction will be negative because they are all exothermic. Do not confuse the two - the amounts are identical but the signs are different.
Thermo Speak
As you venture through thermodynamics you will encounter the terms system, surroundings, and universe. You must have a good picture in your mind of what these are.
The system is what is currently under study. It can be incredibly tiny (a living cell or even a molecule) or immense (an ecosystem or even star system). The surroundings are all the things that are wrapped around the system. Sometimes the border between the system and surroundings is obvious and well defined such as the stainless steel walls of the reaction chamber of a bomb calorimeter. Sometimes the surroundings are completely mixed homogeneously with the system which is the case in solution chemistry (the solvent surrounds each of the solute molecules which are completely dispersed into the solvent). Together, the system and the surroundings make up the universe. For our purposes, the universe is most likely the room we are doing the experiment in. The interaction between system and surroundings is really the immediate surroundings.
We will generally define our systems via chemical reactions (or physical changes) shown as a balanced chemical equation. Such as the combustion of methane shown here
CH4 (g) + 2 O2 (g)
reactants
before
initial
state 1
→
CO2 (g) + 2 H2O (l)
products
after
final
state 2
Below the reaction are four ways of describing the change (read left-to-right on each line). Realize here that when we start, only the methane and oxygen gas are our system. Anything that is not this methane and oxygen must be the surroundings. After the reaction our system is now the carbon dioxide and the water. We must quantify everything so that we can have a complete description of this change. To do this, we need to measure (and report) state functions.
State functions
State functions are qualities or states of a system that are independent of the path by which the system arrived. Anything you can measure as matter “just sits there” is a state function. The main state functions that we constantly concern ourselves with are composition (formula), mass, volume, pressure, and temperature. We have very specific ways to measure each of these. Some ways are easier than others – temperature is easier than composition. In our study of thermodynamics we introduce four more state functions, all of which are pieces of the energy puzzle of matter. The four are internal energy (\(E\)), enthalpy (\(H\)), entropy (\(S\)), and free energy (\(G\)). Each of these energy based state functions will have a unique value for a given set of all the other state functions previously mentioned. What I mean is that if I know that I’ve got say exactly 30 grams of CaCO3 at 25°C under 1 atm pressure then I also am aware of the fact that it also has an exact amount of internal energy, enthalpy, entropy, and free energy also. Do I know those actual values? Maybe, but usually not. For example, I do know a specific formula for the internal energy of an ideal monatomic gas, it is simply
\[E = {3\over 2}RT \]
This is a rare case where we can get the absolute value for \(E\). Typically, real substances are not always gases and are certainly not “ideal”. Real substances have real intermolecular attractions/repulsions that push these energetic state functions to all sorts of possibilities. So how do we get these thermodynamic state functions to reveal themselves? We initiate a change and in doing so we measure \(\Delta E\), \(\Delta H\), \(\Delta S\), and \(\Delta G\). All these \(\Delta\)-values reveal themselves when matter undergoes change. Any physical or chemical change within matter will yield probable changes in these states functions (though not always).
First Law of Thermodynamics (3 ways of saying it)
- The internal energy of an isolated system is constant.
- The energy of the universe is constant.
- Energy can neither be created nor destroyed, only converted in form.
Number 2 above comes from number 1 by assuming that the universe itself is an isolated system. This is true because anything “outside” of the universe would by definition now be know and is part of the universe. Try to avoid some of the metaphysical stuff that finds its way into first law statements. We will be happy enough to realize that our system is typically the reaction or process what we are studying (usually in a reaction chamber of some sort), and our surroundings are the immediate surroundings wrapped around the system.
For number 3 above, realize that matter itself is one of the forms of energy (\(E = mc^2\)). So you could also state that the total amount of energy + matter in the universe is constant. One is often converted into the other – especially in stars, although those are NOT the systems we are concerned with.
Heat and Work
Heat (\(q\)) and work (\(w\)) are not state functions. They are very much path dependent in their values. We will only consider these two forms of energy in our studies. We will also only consider expansion work. Realize there are other forms of energy and different types of work. However, we need not concern ourselves with those until the need arises. For typical endo- and exothermic chemical reactions and physical changes, heat and expansion work are the only energies that we need to track and/or measure.
Internal Energy and Enthalpy
A system will show a change in internal energy only if heat is transferred to/from it and/or work is done on/by it. This is easier to put in equation form
\[\Delta E = q + w \]
where \(q\) is heat that flows in/out of the system and \(w\) is work done on/by the system.
Sign convention is important, all signs (+ or –) are based on the systems point of reference
- heat flowing IN to the system is \(+q\) (energy absorbed – an endothermic process)
- heat flowing OUT of the system is \(-q\) (energy released – an exothermic process)
- work done ON the system is \(+w\)
- work done BY the system is \(-w\)
We define expansion work from the following
\[w=-\int_{V_{\rm initial}}^{V_{\rm final}}PdV\]
so if \(P_{\rm ext}\) (external pressure your system is working against) is constant, work is simply
\[w = -P_{\rm ext}\Delta V \]
and IF that change is due to a reaction containing gases, the Ideal Gas Law (or Avogadro’s Law) tells us that \(P\Delta V = \Delta nRT\) so that work is also defined by
\[w = -\Delta n_{\rm gas}RT \]
where \(\Delta n_{\rm gas}\) is the change in the number of gas moles in the balanced equation of interest. Specifically,
\(\Delta n_{\rm gas}\) = (mol of gas products) − (mol of gas reactants)
Enthalpy is defined as \(H = E + PV\). The book will show you proof that \(\Delta H = q_{\rm P}\). Measure the heat flow from a system at constant pressure and you’ll have the change in enthalpy, \(\Delta H\). Now we get these two equations for constant pressure processes
\[\Delta E = \Delta H - P\Delta V \hskip.5in \Delta E = \Delta H - \Delta nRT\]
Note how you can always get one from the other for \(\Delta E\) and \(\Delta H\) and sometimes they might even be equal (when work is zero).
Heat Capacity
Heat capacity (\(C\)) is the ratio of how energy changes (heat flow) as temperature changes. There are 2 types of heat capacities that we use, one for constant volume processes (which tracks \(q_{\rm v}\)) and one for constant pressure processes (which tracks \(q_{\rm p}\)).
\[\Delta E = q_{\rm v} = n C_{\rm v} \Delta T\] \[\Delta H = q_{\rm p} = n C_{\rm p} \Delta T\]
It is these equations that are used for calorimetry (see Calorimetry help sheet). It is also these equations (the constant pressure one in particular) that we use to track heat in ANY substance (solid, liquid, or gas). Each phase will have its own unique heat capacity. Tables will list heat capacities in 2 different ways or amounts. Many are listed on a per mole basis – these are molar heat capacities. Many are also listed on a per gram basis – these are specific heat capacities. Always look at the units on a measurement to know whether it is per mole or per gram or even per device (like an entire calorimeter). Units will tell you what to do. Once again, knowing the difference in extensive properties (heat capacity, \(C_{\rm p}\) in J/K) and intensive properties (molar heat capacity, \(C_{\rm p}\) in J/mol K) will always help you out.
Heat Capacity for Ideal Gases
An ideal gas can absorb energy in different ways if the molecule has structure. Besides the 3 translational modes (x, y, and z directions) which each contribute \({1\over 2}R\) to the heat capacity, a linear molecule can have 2 more modes of rotational motion (rotation about 2 axes). A non-linear polyatomic molecule will have all 3 modes of rotation motion (rotation about 3 axes). Memorize the following three cases for \(C_{\rm v}\). Then you can get the three \(C_{\rm p}\) ones by a modification (add \(R\)) on those. Here they are spelled out for you:
| monatomic | linear or diatomic |
polyatomic non-linear |
|
|---|---|---|---|
| modes of freedom trans + rot |
3 + 0 = 3 | 3 + 2 = 5 | 3 + 3 = 6 |
| \(C_{\rm v}\) | \({3\over2}R\) | \({5\over2}R\) | \({6\over2}R\) |
| \(C_{\rm p}\) | \({5\over2}R\) | \({7\over2}R\) | \({8\over2}R\) |
This is a bit more specific than Table 9.2 in your book. Note that the heat capacity at constant pressure is always larger that the heat capacity at constant volume. Why? Heating a gas at constant pressure leads to expansion and therefore work. That work energy cost must be paid – it is paid with one more \(R\) unit of energy per mole of gas. Note that for solids and liquids there is rarely a distinction between \(C_{\rm v}\) and \(C_{\rm p}\). This is due to the fact that there is very little difference in there values because their volumes do not change significantly with temperature. You can assume that all heat capacities for solids and liquids are constant pressure heat capacities unless told otherwise.
Thermochemistry
Do know how to calculate amount specific \(\Delta H\)’s when given the general \(\Delta H\) of a reaction. Enthalpies of combustion are like this. If fuel A burns to yield 900 kJ of heat per mole of A, then burning 2.5 moles of A would yield 2250 kJ of heat (\(900\times 2.5\)). This is simply reaction stoichiometry with energy listed as another reactant (endothermic) or product (exothermic). This also applies to physical changes (melting and boiling, Chapter 16 section 10 , “Changes of State”).
Isothermal Expansion
If a gas is allowed to expand isothermally and reversibly then the work and heat are shown to be (section 10.2 in your book)
\[w = -nRT \ln \left({V_2\over V_1}\right)\]
\[q = nRT \ln \left({V_2\over V_1}\right)\]
And remember that \(\left({P_1\over P_2}\right)\) can be substituted in for \(\left({V_2\over V_1}\right)\) because Boyle’s Law in in effect.
Also remember that the internal energy of a gas is directly tied to temperature so that for isothermal expansion
\(\Delta E = 0\) and therefore \(q = -w\)
\(\Delta H = 0\) because \(\Delta E = 0\) and \(PV\) is constant
Hess' Law (3 versions)
You can combine any number of reactions (steps) to equal another "overall" reaction. You also sum the energies involved to get the overall energy. This is show via Hess' Law for enthalpy change:
\[\Delta H_{\rm rxn} = \Delta H_1 + \Delta H_2 + \Delta H_3 + \cdots \]When you "flip" a reaction (switch reactants and products) you must change the sign on \(\Delta H\). If you scale a react up or down (double it, half it, etc...), you must also scale the value of \(\Delta H\).
You can use \(\Delta H_{\rm f}^\circ\) for the rxn steps in Hess' Law.
\[\Delta H_{\rm rxn}^\circ =\sum{n\Delta H^\circ_{\rm f} (\rm products)} - \sum{n\Delta H^\circ_{\rm f} (\rm reactants)}\]
Note that the little subscript "f" here means "of formation". A formation reaction is one that produces that compound from just the elements. Please have a look at my Formation Reactions Help Sheet from our Help Sheets page.
You can also get a good approximation of \(\Delta H\) via the summation of bond energies. The concept is the same regardless of what book (or source) you read it from. Here are a few...
From Zumdahl, Chapter 13, section 8. The "D" is for the dissociation energy of the bond. \[\Delta H =\underbrace{\sum{D\:{\rm (bonds\;\;broken)}}}_{\rm energy\;\; required\uparrow} - \underbrace{\sum{D\:{\rm (bonds\;\;formed)}}}_{\rm energy\;\;released\downarrow}\]
From Aktins/Jones, they use "mean bond enthalpies", \(\Delta H_{\rm B}\) \[\Delta H_{\rm rxn}^\circ =\sum{n\Delta H_{\rm B} (\rm reactants)} - \sum{n\Delta H_{\rm B} (\rm products)}\] Of course when using bond energies or enthalpies, you should break only the bonds that need breaking and make the bonds that need making. You don't have to break every bond in the molecule if much of its structure is retained after the reaction.
IMPORTANT: Just remember you must ADD energy to the system (+, endothermic) to break bonds (reactants) and then the system releases energy (-, exothermic) when new bonds are formed (products). It is this reason that the reactants are listed first in the equation above and the products last. This is unlike all the other equations we use.
SECOND LAW
The second law is all about spontaneous change and what drives it forward. A spontaneous change has the tendency to occur. Spontaneity must always have direction associated with it. The 2nd law helps define what that direction is and how we can determine it though entropy.
- Any spontaneous change is accompanied by an increase in universal entropy (\(\Delta S_{\rm univ}\)).
- Some other results of the 2nd Law...
- Heat flows spontaneously from a hot object to a cold one (never the opposite).
- Energy spontaneously disperses from being localized to becoming spread out if it is not hindered from doing so.
- Energy hates being confined. It is the “desire” for energy to disperse that propels us forward. This ever-increasing universal entropy is sometimes called “time’s arrow”.
Boltzmann’s Formula (statistical definition of entropy)
You want a straight up definition of entropy? Then here you go...
\[S = k {\rm ln}W\]
Where \(W\) is the number of microstates for a system and \(k\) is the Boltzmann constant – really just the same as \(R\) except for single molecules instead of moles of molecules. So all you need is the number of microstates and you can get the absolute entropy for any system. How do you count microstates you ask? Well, that is not really that easy. If you pick a real simple system and confine it greatly (say a temperature of absolute zero so that all thermal energies states are zeroed out) then you might have just one possible microstate and then have zero entropy (see “The 3rd Law” on the next page).
However, even at ZERO kelvin there can be more than one microstate based on different positional locations and orientations of molecules. This non-zero entropy at zero kelvin is called residual entropy. We can easily get bogged down here in the statistical complications of probabilities - so what to do? KNOW that yes, positive entropy changes (2nd Law) always favor the most probable outcome. Read through the derivation of all this in section 10.3 and get to the end of it all. Luckily, we (as chemists) can measure changes in entropy via reversible heat flow and temperature.
Entropy via Heat (thermodynamic definition)
An infintesimal change in entropy can be shown simply to be
\[{\rm d}S = {{\rm d}q_{\rm rev}\over T}\]
When integrated over a given path, \(q_{\rm rev}\) is defined and
\[\Delta S = {q_{\rm rev}\over T}\]
 Note that the heat term is for reversible heat flow. There may be multiple paths to take for heat and work - but there is only ONE path that is reversible and it is through that path that we can get a fix on \(\Delta S\). It is also important to remember that if the process is truly reversible then \(\Delta S_{\rm univ}=0\). Why? Because reversible systems simply trade entropy changes in the system for the surroundings. When this is achieved, the system reaches equilibrium which is a state where \(\Delta S_{\rm univ}=0\) (see equilibrium section further down).
Now, if we are simply heating a substance (or group of substances) under constant pressure from one temperature to another without going through any phase changes then the change in entropy can be defined as
\[\Delta S = nC_p \ln \left({T_2\over T_1}\right)\]
Note that is just the integrated form of the previous \({\rm d}S\) equation. Note also that a similar equation can be written for constant volume conditions using \(C_{\rm v}\).
Isothermal change and Entropy
There are 2 basic equations for \(\Delta S\) for isothermal changes. First, if the change is isothermal expansion of a gas you get
\[\Delta S = nR \ln \left({V_2\over V_1}\right)\]
Note that \(\left({P_1\over P_2}\right)\) can be substituted in for \(\left({V_2\over V_1}\right)\) thanks to Boyle’s Law. Now, if the isothermal change is due to a phase change (a transition), then \(q_{\rm rev}\) is the same as \(\Delta H_{\rm trans}\) and we simply get
\[\Delta S_{\rm trans} = {\Delta H_{\rm trans}\over T}\]
Entropy via Look-up Tables
Also, like with Hess’s Law and \(\Delta H_{\rm f}^\circ\)’s, we can use table values for standard molar entropy (\(S^\circ\)) and get the change of entropy for a reaction:
\[\Delta S_{\rm rxn}^\circ =\sum{n S^\circ (\rm products)} - \sum{n S^\circ (\rm reactants)}\]
Note how those are absolute entropies (\(S\)’s not \(\Delta S\)’s). Absolute entropies are possible due to the 3rd law which establishes conditions for true ZERO entropy.
The 3rd Law
The entropy is zero for a perfectly crystalline solid at absolute zero. It is under these conditions that there can only be ONE single energy microstate (\(W = 1\)) for all the molecules in a solid. That is the energy is confined to only one possible arrangement. This is the ultimate LOW entropy condition and is, in fact, the point at which entropy does equal zero thanks to \(S = k {\rm ln}W\).
We discussed \(\Delta S_{\rm univ} = \Delta S_{\rm sys} + \Delta S_{\rm surr}\) in class. You should realize the importance of each part (system and surroundings) when discussing universal entropy. which is the ultimate determining factor for spontaneity.
Equilibrium
Chemical equilbrium is an example of a dynamic equilibrium and not static equilibrium. Know the difference in the two. Static equilibrium is fixed and non-changing – like balancing weights on a balance beam. Dynamic equilibrium has no NET overall change but does have some given processes still proceeding. The process itself proceeds both forwards and backwards at exactly the same rate. Any thing that you are constantly depleting via one process is simultaneously being replenished by another process. Stated chemically, equilibrium is achieved when the forward rate of reaction equals the reverse rate of reaction. That is a purely kinetic argument for equilibrium and we will study reaction kinetics in Chapter 15 in our book (that’s CH302). A complete understanding of equilibrium requires knowledge of both arguments (definitions) for the equilibrium state. The end of Chapter 10 focuses on the other definition of equilibrium which is based purely on thermodynamic state functions. Lets get the thermodynamic argument for equilibrium established though.
The bottom line for the thermodynamic argument lies in the spontaneity of a reaction. 2nd Law dictates what direction of change is the spontaneous direction. We know that indicator to be universal entropy. If \(\Delta S_{\rm univ}\) is positive, you have found a spontaneous process as written. Whatever is positive one direction must be negative going the other direction. One way, spontaneous (downhill) and the other way, non-spontaneous (uphill). There IS a case right in between – neither up or downhill, flat so to speak. Both directions are equally likely to proceed forward. When conditions are met like this then you have a stalemate on universal entropy. It’s that special condition where \(\Delta S_{\rm univ}=0\) and it is the result of achieving equilibrium. Unfortunately tracking both the system and the surroundings to get the universal entropy is a bit tedious. Let’s get ourselves a new state function for the system that allows us to track in a relative way the universal entropy. That new state function is the Gibb's free energy, \(G\), defined as:
\[G = H - T\;S\]
First notice that \(G\) is made up from 3 other state functions. Also check out how \(G\) will change with \(T\). LOOK at the equation, as \(T\) increases, \(G\) must decrease. That was \(G\)... now, with a little reasoning, we find out that we can now switch to \(\Delta G_{\rm sys}\) to track spontaneity. If we hold temperature (\(T\)) and pressure (\(P\)) constant, we get the following for the change in free energy:
\[\Delta G = \Delta H - T\Delta S\]
This allows us to track spontaneity with a purely system state function, \(\Delta G\). It tracks via sign the opposite of the way that \(\Delta S_{\rm univ}\) does because \(\Delta G = -T\Delta S_{\rm univ}\) (see section 10.7 in your text for proof). Now consider the 3 possible outcomes for \(\Delta G\):
\[\Delta G < 0\]
⊖ negative
spontaneous
\[\Delta G = 0\]
zero
equilibrium
\[\Delta G > 0\]
⊕ positive
non-spontaneous
We now have a new standard to judge spontaneity and equilibrium. ALL equilibrium processes must have a free energy change equal to zero. This is the same as saying that all the free energies (that’s plain ol’ \(G\) here) of all the reactants must equal the free energies of all the products – our “stalemate” condition for equilibrium.
Also note how \(\Delta G\)’s sign is controlled by the signs on \(\Delta H\) and \(\Delta S\). There are 4 cases here which are analagous (but opposite sign!) to those for \(\Delta S_{\rm univ}\) which are given in Table 10.6 in section 10.6 of your book. Here is a plot showing the 4 possible cases:
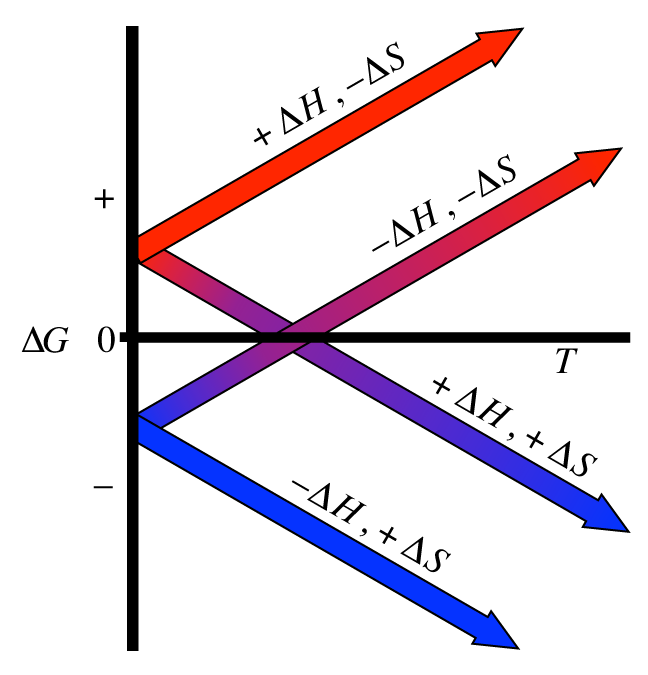
Free energy is a state function and therefore can be calculated via the free energies of formation of the reactants and products just like the enthalpy of reaction was:
\[\Delta G_{\rm rxn}^\circ =\sum{n\Delta G^\circ_{\rm f} (\rm products)} - \sum{n\Delta G^\circ_{\rm f} (\rm reactants)}\]
Most thermodynamic tables include \(\Delta H^\circ_{\rm f}\), \(\Delta G^\circ_{\rm f}\), and \(\Delta S^\circ\), but sometimes you might NOT have \(\Delta G^\circ_{\rm f}\) (like on an exam) and you should know how to calculate \(\Delta G\) from \(\Delta H\) and \(\Delta S\) using the familiar equation:
\[\Delta G = \Delta H - T\Delta S\]
The standard version looks like this:
\[\Delta G^\circ = \Delta H^\circ - T\Delta S^\circ \]
And since \(\Delta H\) and \(\Delta S\) don’t change much with temperature, you can use any temperature (within reason) and calculate non-standard \(\Delta G\). That is:
\[\Delta G \approx \Delta H^\circ - T\Delta S^\circ \]
Remember if you have an equilibrium process occurring, then \(\Delta G = 0\) and therefore
\(\displaystyle{\Delta H = T\Delta S}\) \(\displaystyle{\Delta S = {\Delta H \over T}}\) \(\displaystyle{T = {\Delta H \over \Delta S }}\)
Read the book
Once again I’m asking you to READ. Yes, read your book. You must read over and over to get things straight. Read everything in context. If our book is not getting through to you, go to the chemistry library and read another one. Standard Disclaimer: Any mistakes on this review sheet are NOT intentional. You should crosscheck all stated information. You should double check your book too.

