GOOD TeX Coding
| TeX code | render |
|---|---|
| $\Delta G = \Delta H - T\Delta S$ put whole equations between just 2 $'s |
\(\Delta G = \Delta H - T\Delta S \) this is all math type |
| $q_p = n C_{\rm m} \Delta T$ | \(q_{\rm p} = n C_{\rm m} \Delta T\) |
| H$_2$O(g) | \({\rm H}_2{\rm O(g)} \) phase is plain text |
| ${\rm {1\over 2}H_2 + {1\over 2}F_2 \rightarrow HF} $ | \({\rm {1\over 2}H_2 + {1\over 2}F_2 \rightarrow HF} \) |
| $\Delta H_{\rm f}$ | \(\Delta H_{\rm f} \) |
| $\Delta G^\circ_{\rm f}$ | \(\Delta G^\circ_{\rm f} \) |
| ${\rm 2NO(g) \rightleftharpoons N_2O_4(g)$ note the "equilibrium" arrow |
\({\rm 2NO(g) \rightleftharpoons N_2O_4(g)} \) |
| pH = p$K_{\rm a} + \log\left({C_{\rm A-}\over C_{\rm HA}}\right)$ note the log term and the big parentheses |
\({\rm pH = p}K_{\rm a} + \log\left({C_{\rm A-}\over C_{\rm HA}}\right) \) |
BAD TeX Coding
| TeX code | render |
|---|---|
| $\Delta$ G = $\Delta$ H - T$\Delta$ S don't break up the equation |
\(\Delta {\rm G =} \Delta {\rm H - T}\Delta {\rm S}\) this is not math type |
| q$_p$ = n C$_{\rm m}$ $\Delta$ T | \({\rm q}_p{\rm = n C}_m \Delta{\rm T}\) |
| H$_2$O$_{(g)}$ | \({\rm H}_2{\rm O}_{(g)}\) don't subscript phase |
| 1/2 H$_2$ + 1/2 F$_2$ $\rightarrow$ HF |
\({\rm 1/2H}_2{\rm + 1/2F}_2 \rightarrow {\rm HF} \) |
| $\Delta$H$_f$ | \(\Delta{\rm H}_f \) |
| $\Delta$G$^\circ$$_f$ | \(\Delta{\rm G}^\circ_f \) |
| ${\rm 2NO(g) \leftrightharpoons N_2O_4(g)}$ equilibrium arrow is the wrong way |
\({\rm 2NO(g) \leftrightharpoons N_2O_4(g)} \) |
| $pH = pK_a + log\left({C_{A-}\over C_{HA}}\right)$ | \(pH = pK_a + log\left({C_{A-}\over C_{HA}}\right) \) way too much mathtype |
Just some more TeX coding for various things...
Sometimes you'd prefer to use a root sign instead of parentheses and a fractional power. How about the 3rd root of 27 equaling 3?
$\root 3 \of {27} = 3$ which gives: \(\root 3 \of {27} = 3\)
$(27)^{1/3}=3$ which gives: \((27)^{1/3}=3\)
need bigger/taller parentheses?
$\left({500\over 4}\right)^{1\over 3} = 5$ which gives: \(\left({500\over 4}\right)^{1\over 3} = 5\)
Solving for molar solubility x for a 1:3 salt like Fe(OH)3.
$x=\root 4 \of {K_{\rm sp}\over 27}$ which gives \(x=\root 4 \of {K_{\rm sp}\over 27}\)
TeX Tables
Tables are complicated and require some higher TeX skill. These do not work with MathJax.
$$\vbox{\offinterlineskip\halign{
\strut\hfil#\enskip\hfil
&\hfil\enskip$#$&$.#$\enskip\hfil&\hfil\enskip$#$&$.#$\enskip\hfil&\hfil\enskip$#$&$.#$\enskip\cr
\noalign{\hrule\smallskip}
\#&\multispan 2\hfil [A]\enskip\hfil&\multispan 2\hfil [B]\enskip\hfil&\multispan 2\hfil rate (M/s)\enskip\hfil\cr
\noalign{\smallskip\hrule\smallskip}
1&0&10 &0&10 &7&5\times 10^{-7}\cr
2&0&20 &0&20 &30&0\times 10^{-7}\cr
3&0&20 &0&40 &60&0\times 10^{-7}\cr
\noalign{\smallskip\hrule}
}}$$
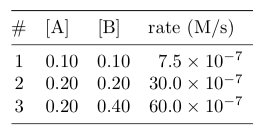
TeX Table Render
The table renders nicely in a TeX document.