Review Sheet - Exam 2 - CH302 - McCord


final version 1.0 (3/1/12) 12:45 PM

Textbook Chapters for Exam 2

In general, we have covered Chapters 6, 7, and 8 for Exam 2. In addition to those chapters, we covered sections 10.10 and 10.11 from Chapter 10. As for what was skipped, here is the best I can tell... we skipped sections 7.8, 7.9, and 7.10 from Chapter 7. We skipped (or have yet to cover) sections 8.3, 8.8, 8.9, and 8.10 from Chapter 8. You’re responsible for any material covered in class whether it was on the homework or not. This review sheet covers most everything we have done. Also remember that no equations are given on the exams. Values for equilibrium constants are given where needed although you should know the value of \(K_{\rm w}\) at 25°C (\(1.0\times 10^{-14}\)).

REMINDER! No graphing calculators for the exam. No formulas will be given on the exam. You do not get to bring a formula sheet. So KNOW your formulas. I will provide any constants that are needed.

Chemical Equilibrium

You still must know how to WRITE the mass action expression
. How does this expression change and the value of K when a reaction is "flipped", doubled, halved?
 What is the value of K when reactions are combined? When is the mass action expression equal to Q? When is it equal to K ?

What is thermodynamic \(K\)? How does that relate to \(K_{\rm p}\) and \(K_{\rm c}\)?

How does \(K_{\rm p}\) relate to \(K_{\rm c}\) ? When would they be equal?
 The formula for this is :

\[K_{\rm p} = K_{\rm c}(RT)^{\Delta n}\]

NOTE: you MUST use the L atm version of \(R\) here - like you did with ideal gases (\(R = 0.08206\) L atm/mol K)

Remember that from Chapter 10 we learned about how free energy and equilibrium were related. Remember that \(\Delta G = 0\) is a criteria for equilibrium. That is \(\Delta G\) without the little superscript circle which means at non-standard conditions. However, it is standard free energy (\(\Delta G^\circ\)) that converts directly to \(K\).

\[\Delta G = \Delta G^\circ + RT \ln(Q) \] \[\Delta G^\circ = -RT \ln(K) \]


This is the Chapter 10 stuff in sections 10 and 11 — you might even have to back up a bit and reread section 9. Make sure your \(R\) units match \(\Delta G\) units. To do this you will probably switch \(\Delta G\) from kJ/mol to just J/mol and then use \(R = 8.314\) J/mol K as your version of \(R\).

What are the units for an equilibrium constant? Technically speaking, there are no units. Why? Read the section on activities. ALL "true" equilibrium constants come from thermodynamics (\(\Delta G^\circ\)) which gives a "plain" \(K\) for equilibrium constant. We make some simple assumptions about activities and concentrations and then just switch to concentrations and/or pressures for our "new" equilibrium constants, \(K_{\rm p}\) and \(K_{\rm c}\). Zumdahl refers to “apparent” units in places, I prefer to stick with the “true” no-unit version which comes out of thermodynamics. So remember, the values for concentration and pressure are acting as substitutes for activities.

Calculations Involving the Equilibrium Constants, \(K_{\rm p}\) and \(K_{\rm c}\)

Know how to calculate the equilibrium constant if given equilibrium amounts of reactants and products. This is where you are given the entire bottom row “e” (final equilibrium concentrations) of the equilibrium table (ICE Table) that we use.

Know how to calculate the equilibrium constant if given initial concentrations and ONE final concentration at equilibrium. This is where you are given only ONE of the bottom row concentrations of your equilibrium table. Remember that knowing only ONE final concentration, you will KNOW the value of \(x\) in your ICE Table.

Know how to calculate final (equilibrium) concentrations if given initial concentrations and the value of \(K_{\rm p}\) or \(K_{\rm c}\). This is the typical type problem where you must set up and solve the equilibrium expression for \(x\). Your entire bottom row will be lots of concentration formulas containing \(x\). You might even have to use the quadratic equation to solve for \(x\) here.

Le Chatelier's Principle

Le Chatelier's Principle: a system at equilibrium will respond to stress so as to relieve the stress.

"Relief" in the statement above comes via the reaction pushing forward or in reverse. The goal is to always regain the equilibrium state. That goal is best thought of here as when \(Q=K\). So anytime a system is out of equilibrium, then \(Q\ne K\).

To regain the equilibrium state you must compare the current value of \(Q\) to \(K\) for the reaction. There are only three possibilities and outcomes here:
\(Q < K\)     rxn forward, RIGHT
\(Q = K\)     at equil, NC
\(Q > K
\)     rxn backward,
 LEFT

Realize that the afore mentioned stress to the system is what typically knocks the system out of the equilibrium state. What are the possible stresses? ANYTHING that takes a system OUT of equilibrium. ANYTHING that forces \(Q\ne K\). The stresses are typically concentration changes, pressure changes, temperature changes (\(\Delta H\) is needed), and global volume changes (like compression or expansion of a gaseous system). Remember, the addition of a catalyst is not a stress at all - it just makes the reactions (forward and reverse) go faster. Knowing all this means you have a complete understanding of Le Chatelier's Principle !!!

Van't Hoff Equation

Not only can you predict the direction of the reaction if you know the sign on \(\Delta H\), but you can also calculate the new equilibrium constant. Remember that changing temperature changes \(K\). How does \(K\) change with temperature? The Van’t Hoff Equation - Which looks a lot like the Claussius-Clapeyron equation from exam 1.

\[\ln\left({K_2\over K_1}\right) = {\Delta H \over R}\left({1\over T_1}-{1\over T_2}\right)\]

Acid/Base Theory and Aqueous Equilibria

Know the difference in a strong, weak, and non-electrolytes.

Know your 2 Acid/Base Theories and their definitions. Those are the Arrehenius Theory and the Lowry-Bronsted Theory. We use the latter one for most of our purposes. Lewis theory is the 3rd one and I’ll leave the details of that one for you folks who go on to take organic chemistry - they love Lewis Theory.

Know how to calculate concentrations of ions for strong electrolyte solutions (strong acids and bases fit this criteria).

Memorize the 7 Strong Acids and 8 Strong Bases listed on my help sheet on our web site. Remember, all of these ionize or dissociate 100% when put in water.

Know the autoionization of water. How is it shown? What is the ion product for water? 
Memorize the value of \(K_{\rm w}\) at 25°C, the value is  \(1.0\times 10^{-14}\). Here's the \(K_{\rm w}\) expression:

\[K_{\rm w}={\rm [H^+][OH^-]}\]

Know how to calculate ANY "p" function — pH, pOH, p\(K_{\rm a}\), p\(K_{\rm b}\), p\(K_{\rm w}\), and in general, pX. Of course know how to do the opposite too. Given pH, what is the H+ or H3O+ concentration?

\[ \eqalign { {\rm pH}&={\rm -log[H^+]}\cr {\rm [H^+]}&=10^{-{\rm pH}}\cr }\]

What's the definition of a neutral solution? What is an acidic pH? basic? neutral? How does the pH scale work? What’s the relationship between pH and pOH?

Know acid/base strength trends - that is know how a conjugate strength is related to the parent acid or base strength. Remember that “opposite” in strength for conjugate pairs is really inverse in strength. Strength is quantitatively shown by knowing the value of \(K_{\rm a}\) or \(K_{\rm b}\). Those two values are linked mathematically for any conjugate pair in water:

\[ K_{\rm w} = K_{\rm a} \cdot K_{\rm b}\]

Know how to write and use the mass action expressions for weak acids (\(K_{\rm a}\)) and weak bases (\(K_{\rm b}\)). This also includes the conjugates of each type which would be the salts of a weak acid/strong base (Generic: NaA), and the salts of a weak base/strong acid (Generic: BHCl ).

Be able to calculate the pH of a solution if only given the percent ionization of the acid or base. You should also be able to do the opposite which is to calculate what the value of \(K_{\rm a}\) or \(K_{\rm b}\) is from the percent ionization and concentration given in a problem.

Know when TO USE and when NOT TO USE the approximation for solving quadratics in acid/base equilibria. What is a "reasonable" concentration? I mentioned two useful checks for this "assumption" :

  1. If \(K\lt 10^{-4}\) AND the conc > 0.05 M
  2. If \(\left({conc \over K}\right) \gt 1000\)

These two checks will generally keep you within 2% or so of the "exact" answer using the quadratic formula. The other method I mentioned in class is the "just do it" method. This is where you ALWAYS just try it (the assumption), but then you compare your \(x\) to your concentrations and see if it really is 1% or less of that concentration.

Polyprotic Acids (and Bases)

Be able to write the appropriate stepwise reactions for polyprotic acids and bases. Know how to calculate the concentrations of various deprotonated species for polyprotic acids and bases.

Remember the numbering for polyprotic acids and their conjugates run in opposite directions. The first proton off a diprotic acid (\(K_{\rm a1}\)) is always the LAST proton going ON to the corresponding conjugate base (\(K_{\rm b2}\)).

For a triprotic acid: H3A ⇌ H+ + H2A- matches up with \(K_{\rm a1}\)

The conjugate reaction is H2A- + H2O ⇌ H3A + OH- and matches up with \(K_{\rm b3}\).

The relationship between the two is \(K_{\rm a1} \cdot K_{\rm b3} = K_{\rm w}\).

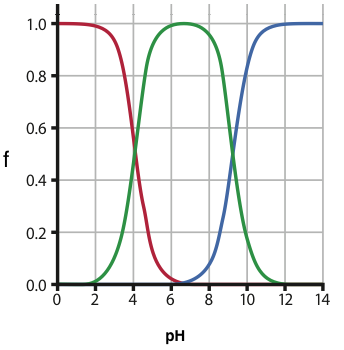
Know what the dominant species are at various pH’s for any acid or base (mono- or polyprotic). Yes, you do have to know the \(K_{\rm a}\)’s or \(K_{\rm b}\)’s, but those would be given. This task is much easier when you know about fraction of species and interpreting its plot vs pH.

Fraction of Species

Know what Fraction of Species is and how to calculate it. Refer to my fraction of species help sheet on our web page. Each fraction of species can be plotted vs pH (see below). Know the way the plot looks and how you would use (interpret) it to answer various questions about what species is the major species at a given pH. Below is a fraction of species plot for a diprotic acid.

Acid / Base Calculations

Know how to calculate the pH (and pOH) for any solution. You should refer to my Acid/Base pdf's that are available on our web page. There are a total of 6 versions of 2 Types of problems…

Chapter 7 problems are what Dr. McCord calls “Type 1” problems. This is when only ONE species is put into solution. There are four possible "species" when dealing with weak acids and bases.

Chapter 8 problems are what Dr. McCord calls “Type 2” problems. This is when there are TWO species put into solution.These two species will be conjugate pairs and the resulting solution will be a buffer.

Chapter 8 – Buffers, pH curves, Titrations, and Indicators

Know the basic premise for making a buffer solution. These are “type 2” problems according to Dr. McCord (see acid/base help sheets on our web site)

Know HOW a good buffer will neutralize both acid and/or base. Yes, this means know the actual reactions that do the neutralizing. 

Be able to use and identify the Henderson-Hasselbalch equations for both acids and bases. There are help sheets for both of these cases available on our web site.

\[{\rm pH} = {\rm p}K_{\rm a} + {\rm log\left({[A^-]\over [HA]}\right)}\] \[{\rm pOH} = {\rm p}K_{\rm b} + {\rm log\left({[BH^+]\over [B]}\right)}\]

Those two equations are exactly correct in that the concentrations shown ARE the equilibrium concentrations. However, on our ICE table we often conclude that the x term is so small, we ignore it when adding or subtracting it to another bigger number. This is known as the "assumption" and can greatly simplify the algebra involved. If the assumption works, then you can directly put in the given (label) concentrations of acid, \(C_{\rm HA}\), and base, \(C_{\rm A^-}\), into the H-H equation as shown below.

\[{\rm pH} \approx {\rm p}K_{\rm a} + {\rm log}\left({C_{\rm A^-}\over C_{\rm HA}}\right)\] \[{\rm pOH} \approx {\rm p}K_{\rm b} + {\rm log}\left({C_{\rm BH^+}\over C_{\rm B}}\right)\] \[{\rm pH} \approx {\rm p}K_{\rm a} + {\rm log}\left({C_{\rm base}\over C_{\rm acid}}\right)\]

Be able to calculate the pH of any buffer, acidic or basic.

What is the common ion effect? Where an ion has more than one source. A- comes a little bit from HA and a lot from NaA, so A- is a common ion.

Know the 2 ways to prepare buffers:

Fraction of Species - Buffers

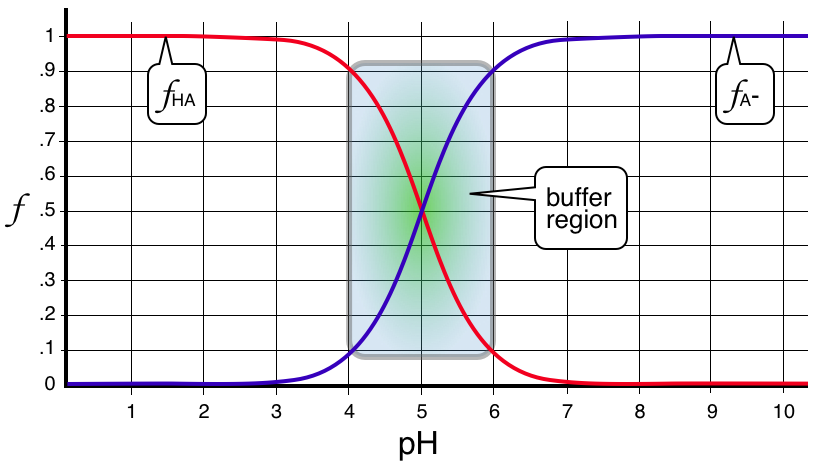
Remember that on a fraction of species diagram the “crossover” region on the plot is the buffer region that is the target for Type 2 calculations. The exact crossover position (intersection) are the special points in pH where the conjugates are equal in concentration and the pH must therefore equal the p\(K_{\rm a}\) - Dr. McCord called this the "perfect buffer" in class.

Now, looking more closely at the diagram, the buffer region is always centered about the pH that equals p\(K_{\rm a}\) for the species. The useful region surrounding that pH is ± 1 pH unit. This is shown on the fraction of species diagram shown below which happens to be for a HA/A- buffer with p\(K_{\rm a}=5.00\).

Buffering Action - Responding to H+ and OH- Stress

Be able to calculate the new pH of a buffer AFTER the addition of strong acid or strong base. Remember that you will always be subtracting from one species and adding to the other in this calculation. For example, if my acid/conjugate base ratio is 35 mmol HA and 35 mmol A- and I add 15 mmol of OH-. After the addition the HA is now 35 - 15 = 20 mmol, and the A- is now 35 + 15 = 50 mmol. That 50/20 ratio is the new ratio that governs the buffer pH. (NOTE: This WAS the iClicker in-class exercise on Monday, 2/27).

Titration Curves

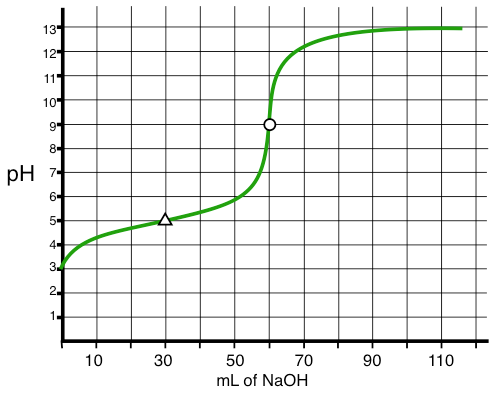
Know how to interpret a pH (titration) curve and get the stoichiometric point (aka: equivalence point) and the p\(K_{\rm a}\) (or p\(K_{\rm b}\)) for a weak acid (or base). Here is a titration curve of a weak acid (\(K_{\rm a}=1.0\times 10^{-5}\)) titrated with strong base.

What's the pH at the stoichiometric point of a titration of a strong acid with strong base? a weak acid with a strong base? a weak base with a strong acid? Know the answer to this in general first - is the pH equal to, greater than, or less than 7.00 (no calculation necessary). Then know the answer exactly which means you’d have to actually calculate the answer.

Note that on the curve given above the stoichiometric point is where the circle is on the plot (at 60 mL and a pH = 9). Also important is the pH at the halfway point which is shown by the triangle on the curve (30 mL and pH = 5). This point is important because the pH here is equal to the p\(K_{\rm a}\) of the acid.

Be able to calculate all the points on a titration curve (pH curve). This really means you now have a full knowledge of acid/base theory from start to finish. You start with only HA (chapter 7 stuff, Type 1 equations), you titrate a bit and now have a buffer (Chapter 8, buffer stuff, Type 2 equations), you then reach the stoichiometric point (back to Type 1 equations - now the conjugate of what you started with), and finally you keep going and overshoot the end point (governed only by excess titrant).

Indicators

Know how indicators work and how to chose the correct indicator for a given titration.

Know the approximate range of an indicator (in general, when given \(K_{\rm a}\)). Remember, the center of its range is where pH = p\(K_{\rm a}\) for the indicator. The range is ±1 off the p\(K_{\rm a}\) value. There are 2 help sheets on our web site about indicators. 

What color will an indicator be at a given pH? (you would know the \(K_{\rm a}\)). Is it red? yellow? orange? yellowish orange? bluish green? reddish purple? ... you get the idea. Remember to split the 2 pH-unit range into 3 regions: ±0.3 is the center and is the “perfect” blend color (like green). Outside of that range and up to ±1 is the “-ish” colors (like bluish-green, or yellowish-green). Outside the ±1 are the straight colors (blue and yellow). Here is a figure illustrating this concept:

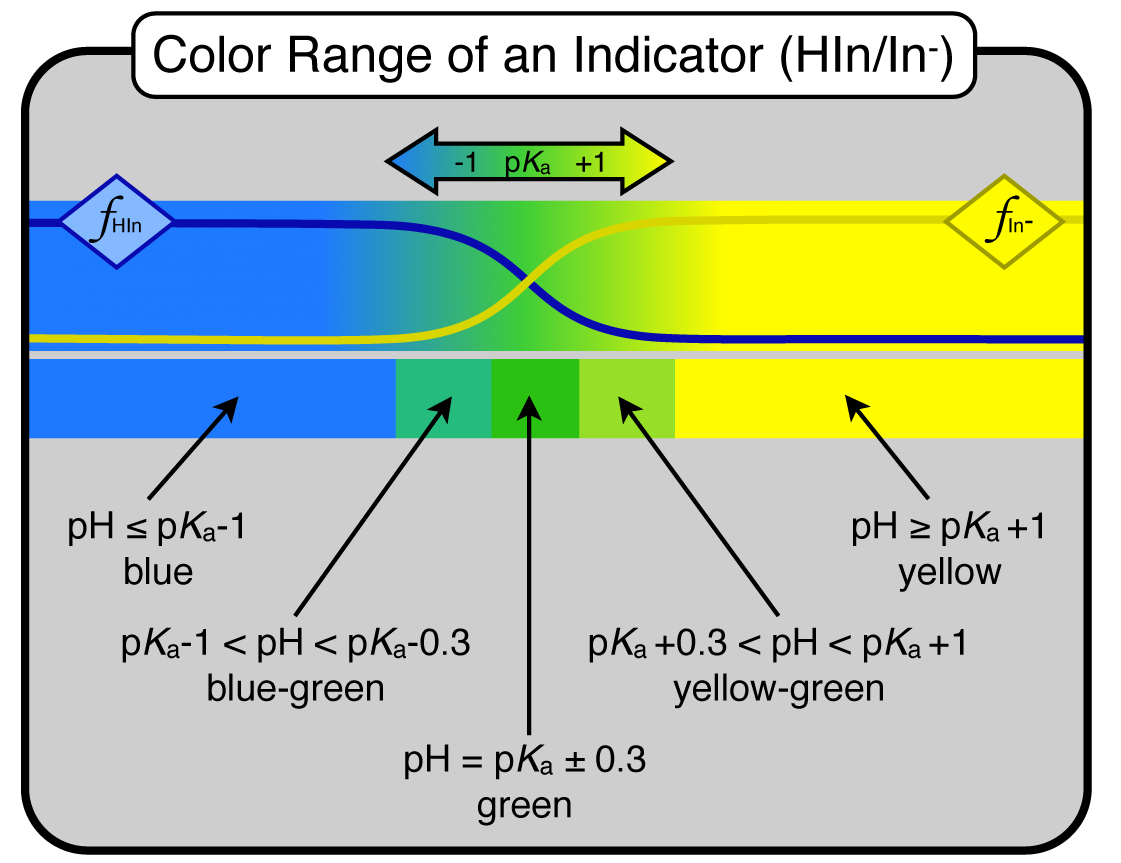
Note in the figure above that there is a fraction of species diagram at the top that shows the fractions of the two conjugates. Remember that the conjugates are two different colors (here, blue and yellow). The crossover region (buffer zone) of the indicator is where all the blends of blue and yellow go. The "blend" of blue and yellow is green. Instead of knowing 10 different shades of green, we break it into just 3 regions: blue-green, green, and yellow-green. Just like with a set of crayons.

Realize that you can have polyprotic acids in the mix for all of the above information. If you make a buffer with a polyprotic acid/base you need to know WHICH \(K_{\rm a}\) to use. Answer, look at which conjugate pairs are the dominant species. Once you know which pair, you know which \(K_{\rm a}\) to use.

I also pointed out in class how useful a fraction of species diagram is for a titration (and buffer formation). I pointed out equivalent points on both the fraction of species diagram and a pH curve. Fraction of species plots are really very helpful in helping you visualize the various species and their various amounts at different pHs. This was mentioned previously in this review sheet.

Now your turn

Now you start writing about all this stuff. Read your book. Over and over. Read other books if you need more help and insight. The more you expose yourself to the concepts the more things will make sense.

Remember, I didn’t purposely leave anything out here to trick you on the exam. If I talked about it in class it is fair game on the exam. Practice working problems in the book and on the homework.

Don’t forget that the questions in your book are an excellent resource for learning. You just have to make yourself do them.